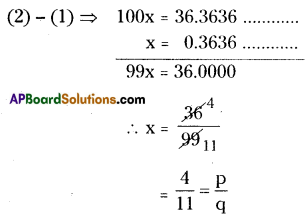8th .Rational Numbers

  Navodaya

Skip to content

1.Rational  Numbers

Click here to get the app 

Click here to get the app 

Rational Numbers

 A number is called Rational if it can be expressed in the form p/q where p and q are integers (q > 0). It includes all natural, whole number and integers.

Example: 1/2, 4/3, 5/7,1 etc. 

Natural Numbers

All the positive integers from 1, 2, 3,……, ∞.

Whole Numbers

All the natural numbers including zero are called Whole Numbers.

Integers

All negative and positive numbers including zero are called Integers.

Properties of Rational Numbers

1. Closure Property

Click here to get the app 

This shows that the operation of any two same types of numbers is also the same type or not.

a. Whole Numbers

If p and q are two whole numbers then

Operation	Addition	Subtraction	Multiplication	Division
Whole number	p + q will also be the whole number.	p – q will not always be a whole number.	pq will also be the whole number.	p ÷ q will not always be a whole number.
Example	6 + 0 = 6	8 – 10 = – 2	3 × 5 = 15	3 ÷ 5 = 3/5
Closed or Not	Closed	Not closed	Closed	Not closed

b. Integers    If p and q are two integers then

Operation	Addition	Subtraction	Multiplication	Division
Integers	p+q will also be an integer.	p-q will also be an integer.	pq will also be an integer.	p ÷ q will not always be an integer.
Example	- 3 + 2 = – 1	5 – 7 = – 2	- 5 × 8 = – 40	- 5 ÷ 7  = – 5/7
Closed or not	Closed	Closed	Closed	Not  closed

c. Rational Numbers

If p and q are two rational numbers then

Operation	Addition	Subtraction	Multiplication	Division
Rational Numbers	p + q will also be a rational number.	p – q will also be a rational number.	pq will also be a rational number.	p ÷ q will not always be a rational number
Example				p ÷ 0 = not defined
Closed or Not	Closed	Closed	Closed	Not closed

2. Commutative Property

This shows that the position of numbers does not matter i.e. if you swap the positions of the numbers then also the result will be the same.

a. Whole Numbers

If p and q are two whole numbers then 

 

Operation	Addition	Subtraction	Multiplication	Division
Whole number	p + q = q + p	p – q ≠ q – p	p × q = q × p	p ÷ q ≠ q ÷ p
Example	3 + 2 = 2 + 3	8 –10 ≠ 10 – 8 – 2 ≠ 2	3 × 5 = 5 × 3	3 ÷ 5 ≠ 5 ÷ 3
Commutative	yes	No	yes	No

3. Associative Property

This shows that the grouping of numbers does not matter i.e. we can use operations on any two numbers first and the result will be the same.

a. Whole Numbers

If p, q and r are three whole numbers then

Operation	Addition	Subtraction	Multiplication	Division
Whole number	p + (q + r) = (p + q) + r	p – (q – r) = (p – q) – r	p × (q × r) = (p × q) × r	p ÷ (q ÷ r)  ≠ (p ÷ q) ÷ r
Example	3 + (2 + 5) = (3 + 2) + 5	8 – (10 – 2) ≠ (8 -10) – 2	3 × (5 × 2) = (3 × 5) × 2	10 ÷ (5 ÷ 1) ≠ (10 ÷ 5) ÷ 1
Associative	yes	No	yes	No

b. Integers

If p, q and r are three integers then

Operation	Integers	Example	Associative
Addition	p + (q + r) = (p + q) + r	(– 6) + [(– 4)+(–5)] = [(– 6) +(– 4)] + (–5)	Yes
Subtraction	p – (q – r) = (p – q) – r	5 – (7 – 3) ≠ (5 – 7) – 3	No
Multiplication	p × (q × r) = (p × q) × r	(– 4) × [(– 8) ×(–5)] = [(– 4) × (– 8)] × (–5)	Yes
Division	p ÷ (q ÷ r) ≠ (p ÷ q) ÷ r	[(–10) ÷ 2] ÷ (–5) ≠ (–10) ÷ [2 ÷ (– 5)]	No

c. Rational Numbers

If p, q and r are three rational numbers then

Operation	Integers	Example	Associative
Addition	p + (q + r) = (p + q) + r		yes
Subtraction	p – (q – r) = (p – q) – r		No
Multiplication	p × (q × r) = (p × q) × r		yes
Division	p ÷ (q ÷ r)  ≠ (p ÷ q) ÷ r		No

The Role of Zero in Numbers (Additive Identity)

Zero is the additive identity for whole numbers, integers and rational numbers.

	Identity		Example
Whole number	a + 0 = 0 + a = a	Addition of zero to whole number	2 + 0 = 0 + 2 = 2
Integer	b + 0 = 0 + b = b	Addition of zero to an integer	False
Rational number	c + 0 = 0 + c = c	Addition of zero to a rational number	2/5 + 0 = 0 + 2/5 = 2/5

Rational Numbers between Two Rational Numbers

Method 1

Example

Find the rational number between 1/10 and 2/10.

Solution

As we can see that there are no visible rational numbers between these two numbers. So we need to write the equivalent fraction.

2/10 = 20/100((multiply the numerator and denominator by 10)

Hence, 2/100, 3/100, 4/100……19/100 are all the rational numbers between 1/10 and 2/10.

Method 2

Find the rational number between 1/10 and 2/10.

Solution

To find mean we have to divide the sum of two rational numbers by 2.

3/20 is the required rational numbers and we can find more by continuing the same process with the old and the new rational number.

Complete Chapter Notes And  (Live) Classes Click below 

Click here to get the app 

Question 1.
Name the properly Involved in the following examples.
vii) 7a + (-7) = 0
viii) x + 1x = 1(x ≠ 0)
ix) (2 x x) + (2 x 6) = 2 x (x + 6)
Solution:
i) Additive identity
ii) Distributive law
iii) Multiplicative identity
iv) Multiplicative identity
v) Commutative law of addition
vi) Closure law in multiplication
vii) Additive inverse
viii) Multiplicative inverse
ix) Distributiv

Question 2.
Write the additive and the multiplicative inverses of the following.
i) −35
ii) 1
iii) 0
iv) 79
v) -1
Solution:

Click here to get the app 

Question 3.
Fill in the blanks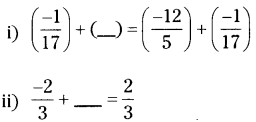



Solution

Click here to get the app 

Question 4.
211×(−145)=−2855

Click here to get the app 

Question 5.
Which properties can be used computing 25×(5×76)+13×(3×411)
Solution:
The following properties are involved in the product of
25×(5×76)+13×(3×411)
i) Multiplicative associative property.
ii) Multiplicative inverse.
iii) Multiplicative identity.
iv) Closure with addition

Click here to get the app 

Question 6.
Verify the following
(54+−12)+−32=54+(−12+−32)
Solution:

Click here to get the app

Question 7.
Evaluate 35+73+(−25)+(−23) after rearrangement.
Solution:

     Click here to get the app

Question 8.
Subtract
(i) 34 from 13
(ii) −3213 from 2
(iii) -7 from −47
Solution:

Click here to get the app

Question 9.
What numbers should be added to −58 so as to get −32 ?
Solution:
Let the number to be add ‘x’ say

∴ −78 should be added to −58 then we will get −32

Click here to get the app

Question 10.
The sum of two rational numbers is 8 If one of the numbers is −56 find the other.
Let the second number be ‘x’ say
⇒ x+(−56)=8
⇒8+56=48+56=536
∴ The other number (x) = 536

Click here to get the app

Question 11.
Is subtraction associative in rational numbers? Explain with an example.
Solution:
Let 12,34,−54 are any 3 rational numbers.
Associative property under subtraction
a – (b – c) = (a – b) – c

∴ L.H.S. ≠ R.H.S.
∴ a – (b – c) ≠ (a – b) – c
∴ Subtraction is not an associative in rational numbers.

Question 12.
Verify that – (-x) = x for
(i) x = 215
(ii) x = −1315
Solution:

Click here to get the app

Question 13.
Write-
(i) The set of numbers which do not have any additive identity
(ii) The rational number that does not have any reciprocal
(iii) The reciprocal of a negative rational number.
Solution:
i) Set of natural numbers ’N’ doesn’t possesses the number ‘0’.
ii) The rational number ‘0’ has no multiplicative inverse.
[ ∵ 1/0 is not defined]
iii) The reciprocal of a negative rational number is a negative rational number.
Ex : Reciprocal of −25=−52

Click here to get the app 

Exercise 1.2

Question 1.
Represent these numbers on the number line.
(i) 97
(ii) −75
Solution:
(i) 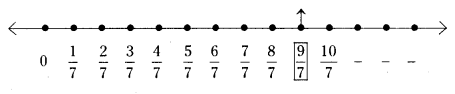97

(ii) −75

Question 2.
Represent −213,513,−913 on the number line.
Solution:

Click here to get the app

Question 3.
Write five rational numbers which are smaller than 56
Solution:
The rational number which are less than
56={46,36,26,16,06,−16,−26…….}

Click here to get the app

Question 4.
Find 12 rational numbers between -1 and 2.
Solution:

Click here to get the app

Question 5.Find a rational number between 

23 nd 34
[Hint : First write the rational hu numbers with equal denominators.]
Solution:
The given rational numbers are 23 and 34
23×44=812,34×33=912
The rational numbers between 812,912 is
(812+912)2=17122=1724
(∵ the rational number between a, b is a+b2 )
∴ the rational number between 23 and 34 is 1724

Click here to get the app

Question 6.
Find ten rational numbers between −34 and 56
Solution: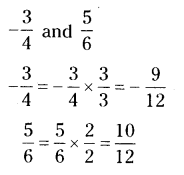

The 10 rational numbers between −912 and 1012 are

∴ We can select any 10 rational numbers from the above number line.

Click here to get the app

Exercise 1.3

Click here to get the app

Question 1.
Express each of the following decimal in the pq form.
(i) 0.57 (ii) 0.176 (iii) 1.00001 (iv) 25.125
Solution:

Click here to get the app

Question 2.
Express each of the following decimals in the rational form pq
(1) 0.9¯¯¯
(ii) 0.57¯¯¯¯¯
(iii) 0.729¯¯¯¯¯
(iv) 12.28¯¯¯
Solution:
(i) Let x =  0.999 ………………. (1)
Here periodicity is 1. So, equation (1) should be multiplied both sides with
= 10 × x = 10 × 0.999
10 x = 9.999 ………….. (2)

(ii) x = 0.57¯¯¯¯¯ ⇒ x = 0.5757…………(1)
Here periodicity is 2. So, we should multiply with 100
⇒ 100 × x = 100 x 0.5757 …………..
100 × =57.57 ……………………. (2)

(iii) 0.729¯¯¯¯¯
x = 0.729¯¯¯¯¯
x = 0.729¯¯¯¯¯ ⇒ x = 0.7979…………(1)
Here periodicity is 2. So, equation (1) should multiply with 100
⇒ 100 × x = 100 × 0.72929 …………..
100 × = 72.929 …………………… (2)

Click here to get the appi

Iv) 

⇒ x = 12.288 ………..(1)
Here periodicity is 1. So, equation (1) should multiply with 10
10 x = 122.888 …………………… (2)

Click here to get the app

Question 3.
Find(x + y) ÷ (x – y) if
(i) x = 52, y = −34
(ii) x = 14, y = 32
Solution:If x = 52, y = −34 then

ABCD

ii) x = 14, y = 32

Question 4.
Divide the sum of −135 and 127 by the product of −137 and −12
Solution:
Sum of −135 and 
the product of −137 and −12

Question 5.
If 25 of a number exceeds 17 of the same number by 36. Find the number.
Solution:
Let the number be ‘x’ say.

∴ According to the sum,

Question 6.
Two pieces of lengths 225 m and 3310 mare cut off from a rope 11 m long. What is the length of the remaining rope?
Soltuion:
The length of the remaining rope Is x

∴ The length of remaining rope
= 5110 mts.

Question 7.
The cost of 723 meters of cloth is ₹1234 . Find the cost per metre.
Solution:
The cost of 723 mts (233 mts ) of cloth
= ₹ 1234 = ₹ 514
∴ The cost of 1m cloth
= 514÷233=514×323=15392 = ₹ 1.66

Question 8.
Find the area of a rectangular park which is 1835m long and 823 in broad.
Solution:
The length of the rectangular park
= 1835m = 935
Its width / breath = 823 m = 263 m
∴ Area of the rectangular park
(A) = l × b

Question 9.
What number should −3316 be divided by to get −114
Solution:
Let the dividing number be ‘x’ say.

Question 10.
If 36 trousers of equal sizes can be stitched with 64 meters of cloth. What is the length of the cloth required for each trouser?
Solution:
36 trousers of equal sizes can he stitched with 64 mts of cloth, then the length of the cloth ¡s required for each trouser
= 64 ÷ 36
= 6436=169 = 1 79

Question 11.
When the repeating decimal 0.363636 …. is written in simplest fractional formpq , find the sum p+ q.
Solution:
x = 0.363636………………………….. (1)
Here periodicity is ‘2’. So, equation (1) should be multiplied both sides with 100.
⇒ 100 × x = 100 × 0.363636 …………..
100 x = 36.3636 ………..(2)