Skip to content
Fractions
Fractions
Fractions are numbers representing part of a whole.
A fraction is a number of the form p/q, such that q is not equal to zero or one.
A fraction has two parts. The number on the top is numerator and the number below is the denominator.

The numerator can be greater or smaller than the denominator.
For e.g. 1/5th of a pizza is a fraction , that is, written as 1/5.

Types of Fractions
There are three major types of fractions:
- Proper Fraction
- Improper Fraction
- Mixed Fraction
Proper Fractions
Fractions where numerator is always less than the denominator.
It is called proper because the number of parts will always be lesser than the total number of parts. For e.g. 1/3, 1/6, 2/7, 9/10 and so on.
The value of a proper fraction will always be less than 1.
Improper Fractions
Fractions where numerator is always more than the denominator.
It is called improper because the number of parts will be greater than the total number of parts. For e.g. 5/3, 9/6, 8/7, 14/10 and so on.
The value of a proper fraction will always be greater than 1.
Mixed Fraction
Fractions where there is a combination of a whole and a fractional part. For e.g.

All Improper fractions can be expressed as mixed fractions
Like and Unlike Fractions
Like fractions are fractions with same denominator. For eg ½, 15/2, 19/2 and so on.
Unlike fractions are fractions with different denominators. For e.g. 16/5, 7/8, ½, 2/5, 2/10.
It is important to note that like and unlike fractions are decided only on the basis of denominator. The value of numerator does not matter.
Equivalent Fractions
Equivalent fractions are fractions which represent the same number.
For e.g. Tipu divides the pizza into 2 equal halves and eats one half of it. Bhola divides the same pizza into 4 equal halves and eats two parts of it.

Share of Pizza eaten by Bhola = 2 parts out of 4 = 2/4. This can be further reduced to get :
2/4 = ½ = 0.5
Share of Pizza eaten by Tipu = 1 part of out of 2 = ½.
½ = 0.5.
Thus, although the fractions are 2/4 and 1/2 but they represent the same numbers. Hence they are equivalent fractions.
In order to make equivalent number, we have to multiply both the numerator and the denominator by the same number. For eg we get the following fractions when we keep on dividing both the numerator and the denominator by the number 2.

Comparing Fractions
Comparing Like Fractions
In like fractions, the denominators are the same. So, only numerators are compared.
The one with bigger numerator is the bigger fractions.
For e.g. ¾>1/4
Comparing Unlike Fractions
In unlike fractions, denominators are different.
Firstly, we try and make the denominators same.
This is done by converting fractions into equivalent fractions. To do this, the LCM of different denominators.
Each fraction is converted into a form such that the LCM as the common denominator of both the fractions.
Comparison of the like fractions obtained can be done by comparing the numerators.
For e.g.
1/3 and 2/4
LCM of 3 and 4 = 12
Multiply Numerator and denominator of 1/3 by 4 such that the equivalent fraction has 12 in the denominator
1*4/3* 4 = 4/12
Multiply Numerator and denominator of 2/4 by 3 such that the equivalent fraction has 12 in the denominator
2*3/4* 3 = 6/12
Since the denominators are the same, comparing the numerators we get :
4/12 < 6/12
Therefore, 1/3 < 2/4
Problem: Compare the fractions a) 3/b and 5/6 b) 1/7 and 1/4
Solution
3/6 and 5/6 are like fractions because they have common denominators.
5 is greated than 3, so 5/6 is greater than 3/6
1/7 and ¼ are unlike fractions.
Firstly, we try and make the denominators same.
This is done by converting fractions into equivalent fractions. To do this, the LCM of different denominators.
The LCM of 7 and 4 is 28. We get :
1*4/7*4 and 1*7/4*7
4/28 and 7/28
These are like fractions now. Comparing the numerators, we get:
4/28<7/28.
Question 1.
Solve the following.
(i) 2 + 34
(ii) 79+13
(iii) 1 – 47
(iv) 223+12
(v) 58−16
(vi) 223+312
Solution:
Question 2.
Arrange the following in ascending order.
(i) 58,56,12
(ii) 25,13,310
Solution:
Question 3.
Check whether in this square the sum of the numbers in each row and in each column and along the diagonals is the same.
Question 4.
A rectangular sheet of paper is 523 cm long and 315 cm wide. Find its perimeter.
Solution:
Length of the rectangular sheet = 523 cm
Breadth/width of the rectangular sheet = 523 cm
Perimeter = 2 x (length + breadth)
Question 5.
The recipe requires 314 cups of flour. Radha has 138 cups of flour. How many more cups of flour does she need?
Solution:
Flour required for the recipe = 314 cups
Flour with Radha = 138 cups
More cups of flour required = 314−138
Question 6.
Abdul is preparing for his final exam. He has completed 512 part of his course content. Find out how much course content is left?
Solution:
Take content as 1 (i.e., full) Course completed = 512
Course yet to be completed = 1 – 512
= 12×1−512
12−512=712
Question 7.
Find the perimeters of(i) ΔABE (ii) the rectangle BCDE in this figure. Which figure has greater perimetre and by how much?
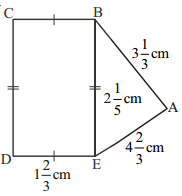
Solution:
i) Perimeter of ΔABE = AB + BE + AE
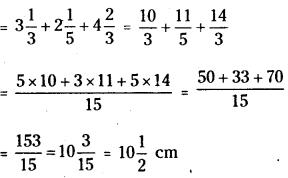
ii) Perimeter of BCDE = 2(BE + BC)
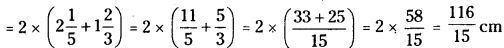
As 11615<15315, we conclude that the perimetre of ΔABE > Perimeter of BCDE
Exercise 2
Skip to contenQuestion 1.
Multiply the following. Write the answer as a mixed fraction.
(i) 36 x 10
(ii) 13 x 4
(iii) 67 x 2
(iv) 29 x 5
(v) 15 x 25
Solution:
(i) 36 x 10 = 306 = 5 i.e., integer part 5; fraclon part = 0
(ii) 13 x 4 = 43 = 113
(iii) 67 x 2 = 127 = 157
(iv) 29 x 5 = 109 = 119
(v) 15 x 25 = 305 = 6 i.e., integer part = 6; fraction part = o
Question 2.
Shade: (i) 12 of the circles in box (a)
(ii) 23 of the triangles in box (b)
(iii) 35of the rectangles in box (c)
(iv) 34 of the circles in box (d)
Question 3.
Find (i) 12 of 12 (ii) 25 of 1
Solution:
(i) 12 of 12 = 12 x 12 = 123 = 4
(ii) 25 of 15 = 25 x 15 = 305 = 6
Question 1.
Find each of the following products.
(i) 56×711
(ii) 6×15
(iii) 213×315
Solution:
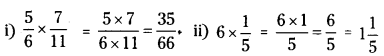
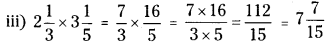
Question 2.
Multiply and reduce to lowest form.
(i) 23×515
(ii) 27×13
(iii) 93×55
Solution:
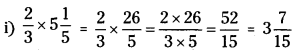
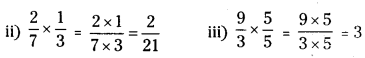
Question 3.
Which one is greater’?
(i) 25 of 47 or 34 of 12
(ii) 12 of 47 or 23 of 37
Solution:
(i) 25 of 47 or 34 of 12














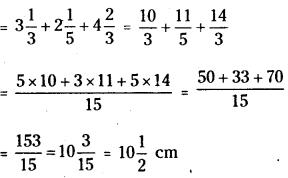


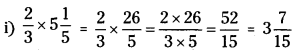
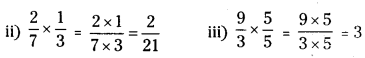

Very nice website easly we get the solution for a problems
ReplyDeleteAnd I got more practice problems in this website. TQ alot to Solutionkey institute