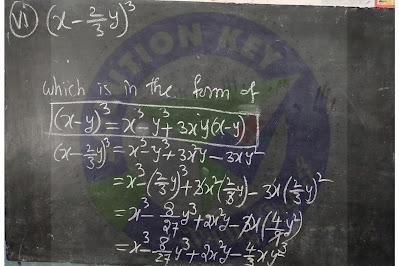Polynomials
(1) Algebraic Expressions : Any expression containing constants, variables, and the operations like addition, subtraction, etc. is called as an algebraic expression.
For example: 5x, 2x – 3, x2 + 1, etc. are some algebraic expressions.
(2) Polynomials : The expression which contains one or more terms with non-zero coefficient is called a polynomial. A polynomial can have any number of terms.
For example: 10, a + b, 7x + y + 5, w + x + y + z, etc. are some polynomials.
Click here to get the app
(3) Polynomials in One Variable : The expression which contains only one type of variable in entire expression is called a polynomial in one variable.
For example: 2x, a2 + 2a + 5, etc. are polynomials in one variable.
(4) Term : A term is either a single number or variable and it can be combination of numbers and variable. They are usually separated by different operators like +, -, etc.
For example: Consider an expression 6x - 7. Then, the terms in this expression are 6x and -
(5) Coefficient : The number multiplied to variable is called as coefficient.
For example: The coefficient of the term 2x will be 2.
(6) Constant Polynomials : An expression consisting of only constants is called as constant polynomial.
For Example: 7, -27, 3, etc. are some constant polynomials.
(7) Zero Polynomial : The constant polynomial 0 is called as zero polynomial.
Want to learn by Video Lectures? CLICK HERE to watch them
* Monomials : The expressions which have only one term are called as monomials.
For Example: p(x) = 3x, q(a) = 2a2, etc. are some monomials.
* Binomials : The expressions which have two terms are called as binomials.
For example: r(x) = x + 10, c(z) = 7z2 + z etc. are some binomials.
* Trinomials : The expressions which have three terms are called as trinomials.
For example: p(x) = 7x2 + x + 7, d(t) = t3 – 3t + 4, etc. are some trinomials.
Degree of polynomial : The highest power of the variable in a polynomial is called as the degree of the polynomial.
For Example: The degree of p(x) = x5 – x3 + 7 is 5.
Note: The degree of a non-zero constant polynomial is zero.
Linear polynomial : A polynomial of degree one is called a linear polynomial.
For Example: 2x – 7, s + 5, etc. are some linear polynomials.
* Quadratic polynomial : A polynomial having highest degree of two is called a quadratic polynomial. In general, a quadratic polynomial can be expressed in the form ax2 + bx + c, where a≠0 and a, b, c are constants.
For Example: x2– 9, a2 + 7, etc. are some quadratic polynomials.
* Cubic polynomial : A polynomial having highest degree of three is called a cubic polynomial. In general, a quadratic polynomial can be expressed in the form ax3 + bx2 + cx + d, where a≠0 and a, b, c, d are constants.
For Example: x3– 9x +2, a3 + a2 + a + 7, etc. are some cubic polynomials.
* General expression of polynomial : A polynomial in one variable x of degree n can be expressed as an xn + an-1 xn-1 + ..... + a1 x + a0, where an ≠ 0 and a0, a1, .... an are constants.
Want to learn by Video Lectures? CLICK HERE to watch them
* Zeroes of a Polynomial : The value of variable for which the polynomial becomes zero is called as the zeroes of the polynomial.
For Example: Consider p(x) = x + 2. Find zeroes of this polynomial.
(i) If we put x = -2 in p(x), we get,
(ii) p(-2) = -2 + 2 = 0.
(iii) Thus, -2 is a zero of the polynomial p(x).
Examples:
For Example: Find value of polynomial 3a2 + 5a + 1 at a = 3.
(i) Here, p(a) = 3a2 + 5a + 1.
(ii) Now, substituting a = 3, we get,
(iii) p(3) = 3 x (3)2 + 5 x 3 + 1 = 27 + 15 + 1 = 43
For Example: Check whether at x = -1/7 is zero of the polynomial p(x) = 7x + 1.
(i) Given, p(x) = 7x + 1.
(ii) Now, substituting x = -1/7, we get,
(iii) p(-1/7) = 7(-1/7) + 1 = -1 + 1 = 0.
(iv) Here, p(-1/7) is zero. Thus, -1/7 is zero of the given polynomial.
For Example: Find zero of the polynomial p(x) = 2x+ 2.
(i) Equating p(x) to zero, we get,
(ii) p(x) = 0
(iii) 2x + 2 = 0
(iv) 2x = -2 i.e. x = -1.
(v) Thus, x = -1 is a zero of the given polynomial.
Want to learn by Video Lectures? CLICK HERE to watch them
Click here to get the app
Remainder Theorem:
Statement: Let p(x) be any polynomial of degree greater than or equal to one and let a be any real number. If p(x) is divided by the linear polynomial x – a, then the remainder is p(a).
Example: Divide 3x2 + x – 1 by x + 1.
(i) Let, p(x) = 3x2 + x – 1 and g(x) = x + 1.
(ii) Performing divisions on these polynomials, we get,(iii) Now, we can re-write p(x) as 3x2 + x – 1 = (x + 1) (3x -2) +1.
For Example: Find remainder on dividing x3 + 3x2 + 3x + 1 by 2x + 5.
Thus, remainder obtained on dividing x3 + 3x2 + 3x + 1 by 2x + 5 is -27/8.
Want to learn by Video Lectures? CLICK HERE to watch them
Factorisation of Polynomials:
(i) Factor Theorem: If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then
(a) x – a is a factor of p(x), if p(a) = 0
(b) p(a) = 0, if x – a is a factor of p(x)
For Example: Check whether (x + 1) is factor of p(x) = x3 + x2 + x + 1.
(i) As per Factor Theorem, (x + 1) is factor of p(x) = x3 + x2 + x + 1, if p(-1) = 0.
(ii) Therefore, p(-1) =(-1)3 + (-1)2 + (-1) + 1 = -1 + 1 -1 + 1 = 0.
(iii) Thus, (x + 1) is factor of p(x) = x3 + x2 + x + 1.
For Example: Find value of k, if (x – 1) is factor of p(x) = kx2 – 3x + k.
(i) As per Factor theorem, here, p(1) = 0.
(ii) So, k(1)2 – 3(1) + k = 0.
(iii) k – 3 + k = 0
(iv) 2k – 3 = 0
(v) k = 3/2.
For Example: Factorise 2y3 + y2 – 2y – 1.
(i) On using trial and error method, we get,
(ii) p(1) = 2(1)3 + (1)2 – 2(1) – 1 = 2 + 1 – 2 -1 = 0.
(iii) Thus, (y – 1) is factor of 2y3 + y2 – 2y – 1.
using division method, we get,
p(y) = 2y3 + y2 – 2y – 1
= (y – 1) (2y2 + 3y + 1)
= (y – 1) (2y2 + 2y + y + 1)
= (y – 1) (2y (y + 1) + 1 (y + 1))
= (y – 1) (y + 1) (2y + 1)
Algebraic Identities:
(i) (a +b) 2 = (a2 + 2ab + b2)
(ii) (a – b) 2 = (a2 - 2ab + b2)
(iii) a2 – b2 = (a + b) (a – b)
(iv) (x + a) (x + b) = x2 + (a + b)x + ab
(v) (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(vi) (a + b)3 = a3 + b3 + 3ab (a + b)
(vii) (a – b) 3 = a3 - b3 - 3ab (a - b) = a3 – 3a2b + 3ab2 - b3
(viii) a3 + b3 + c3 - 3abc = (a + b + c) (a2 + b2 + c2 - ab - bc - ca)
For Example: Use suitable identity to find (x + 2) (x – 3).
(i) We know the identity, (x + a) (x + b) = x2 + (a + b)x + ab
(ii) Using the identity, (x + 2) (x – 3) = x2 + (2 – 3)x + (2)(-3) = x2 – x – 6.
For Example: Evaluate (102 x 107) without multiplying directly.
We know the identity, (x + a) (x + b) = x2 + (a + b)x + ab
(i) Here, we can write, 102 as (100 + 2) and 107 as (100 + 7). So, x = 100, a = 2 and b = 7.
(ii) Using the identity, (102 x 107) = 1002 + (2 + 7)100 + (2)(7) = 10000 + 900 + 14 = 10914
For Example: Factorise (a + b + c)2 = 4a2 + 16b2 + 64c2 + 16ab + 64bc + 32ca.
(i) We know the identity, (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
(ii) Now, 4a2 + 16b2 + 64c2 + 16ab + 64bc + 32ca
= (2a)2 + (4b)2 + (8c)2 + 2(2a)(4b) + 2(4b)(8c) + 2(8c)(2a).
= (2a + 4b + 8c)2
= (2a + 4b + 8c) (2a + 4b + 8c)Ex 2.1
Ex 2.1
Question 1:
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 
(ii) 
(iii)
(iv) 
(v) 
ANSWER:
(i)
Yes, this expression is a polynomial in one variable x.
(ii)
Yes, this expression is a polynomial in one variable y.
(iii)
No. It can be observed that the exponent of variable t in term 
is 
, which is not a whole number. Therefore, this expression is not a polynomial.
(iv)
No. It can be observed that the exponent of variable y in term
is −1, which is not a whole number. Therefore, this expression is not a polynomial.
(v)
No. It can be observed that this expression is a polynomial in 3 variables x, y, and t. Therefore, it is not a polynomial in one variable.
Question 2:
Write the coefficients of 
in each of the following:
(i) 
(ii) 
(iii) 
(iv) 
ANSWER:
(i)
In the above expression, the coefficient of is 1.
(ii)
In the above expression, the coefficient of is −1.
(iii)
In the above expression, the coefficient of is
.
(iv) 
In the above expression, the coefficient of is 0.
Question 3:
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
ANSWER:
Binomial has two terms in it. Therefore, binomial of degree 35 can be written as 
.
Monomial has only one term in it. Therefore, monomial of degree 100 can be written as x100.
Question 4:
Write the degree of each of the following polynomials:
(i) 
(ii) 
(iii) 
(iv) 3
ANSWER:
Degree of a polynomial is the highest power of the variable in the polynomial.
(i)
This is a polynomial in variable x and the highest power of variable x is 3. Therefore, the degree of this polynomial is 3.
(ii)
This is a polynomial in variable y and the highest power of variable y is 2. Therefore, the degree of this polynomial is 2.
(iii)
This is a polynomial in variable t and the highest power of variable t is 1. Therefore, the degree of this polynomial is 1.
(iv) 3
This is a constant polynomial. Degree of a constant polynomial is always 0.
Question 5:
Classify the following as linear, quadratic and cubic polynomial:
(i)
(ii) 
(iii) 
(iv) 
(v) 
(vi) 
(vii) 
ANSWER:
Linear polynomial, quadratic polynomial, and cubic polynomial has its degrees as 1, 2, and 3 respectively.
(i) is a quadratic polynomial as its degree is 2.
(ii) is a cubic polynomial as its degree is 3.
(iii) is a quadratic polynomial as its degree is 2.
(iv) 1 + x is a linear polynomial as its degree is 1.
(v) is a linear polynomial as its degree is 1.
(vi) is a quadratic polynomial as its degree is 2.
(vii) is a cubic polynomial as its degree is 3.
Ex 2.2
Question 1:
Find the value of the polynomial 
at
(i) x = 0 (ii) x = −1 (iii) x = 2
ANSWER:
(i) 
(ii)
(iii)
Ex 2.4
Click here to get the app
Ex 2.5
