Introduction
Expressions that contain only constants are called numeric or arithmetic expressions.
Expressions that contain only constants are called numeric or arithmetic expressions.
Expressions that contain constants and variables, or just variables, are called algebraic expressions.
While writing algebraic expressions, we do not write the sign of multiplication. An algebraic expression
containing only variables also has the constant 1 associated with it. The parts of an algebraic expression
joined together by plus (+) signs are called its terms.
A term that contains variables is called a variable term.
A term that contains only a number is called a constant term. The constants and the variables whose
product makes a term of an algebraic expression, are called the factors of the term. The factors of a
constant term in an algebraic expression are not considered. The numerical factor of a variable term
is called its coefficient. The variable factors of a term are called its algebraic factors.
Terms that have different algebraic factors are called unlike terms. Terms that have the same algebraic
factors are called like terms. Algebraic expressions that contain only one term are called monomials.
Algebraic expressions that contain only two unlike terms are called binomials. Algebraic expressions
that contain only three unlike terms are called trinomials. All algebraic expressions that have one or
more terms are called polynomials. Therefore, binomials and trinomials are also polynomials.
Exercise 11.1
Question 1.
Find the product of the following pairs:(i) 6, 7k
(ii) – 31, – 2m
(iii) -5t2 – 3t2
(iv) 6n, 3m
(v) – 5p2, – 2p
Solution:
The product of 6, 7k = 6 × 7k = 42k
ii) The product of – 3l, – 2m = (- 3l) × (- 2m) = 6/m
iii) The product of – 5t2, – 3t2 = (- 5t2) × (- 3t2) = 15t4
iv) The product of 6n, 3m = 6n × 3m = 18mn
v) The product of – 5p2, – 2p = (- 5p2) × (- 2p) = 10p3
Complete the table of the products.Solution:
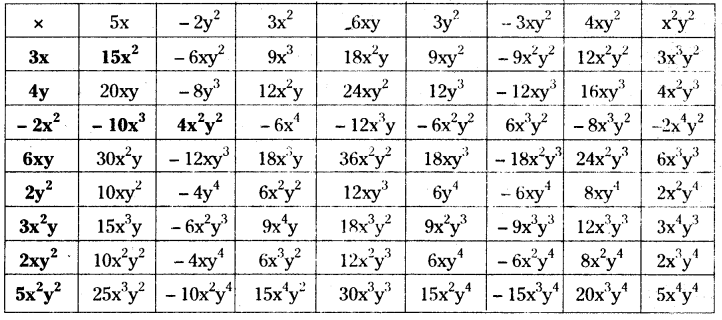
Question 3.
Find the volumes of rectangular boxes with given length, breadth and height in the following table.
Question 4.
Find the product of the following monomials
(i) xy, x2y , xy, x
(ii) a, b, ab, a3 b, ab3
(iii) kl, lm, km, klm
(iv) pq ,pqr, r
(v) – 3a, 4ab, – 6c, d
Solution:
i) The product of xy, x2y, xy, x = xy × x2y × xy × x
= x5 × y3= x5y3
ii) The product of a, b, ab, a3b, ab3 = a × b × ab × a3b × ab3
= a6 × b6 = a6 b6
iii) The product of kl, lm, km, klm = kl × lm × km × klm
k3 × l3 × m3 =k3l3m3
iv) The product of pq, pqr, r = pq × pqr × r
= p2 × q2 × r2 – p2q2r2
v) The product of – 3a, 4ab, – 6c, d = (- 3a) × 4ab × (- 6c) x d
= + 72a2 × b × c × d
= 72a2bcd
Question 5.
If A = xy,B = yz and C = zx, then find ABC=
Solution:
ABC = xy × yz × zx = x2y2z2
Question 6.
If P = 4x2, T = 5x and R = 5y, then
Solution:
Question 7.
Write some monomials of your own and find their products.
Solution:
The product of,some monomials is given below :
i) abc × a2bc = a3b2c2
ii) xy × x2z × yz2 = x3y2z3
iii) p × q × r = p3q3r3
Exercise 11.2
Complete the table:
Question 2.
Simplify: 4y(3y + 4)
Solution:
4y(3y + 4) = 4y × 3y + 4y × 4
= 12y2 + 6y
Question 3.
Simplify x(2x2 – 7x + 3) and find the values of it for (i) x = 1 and (ii) x = 0
Solution:
x(2x2 – 7x + 3)
= x × 2x2 – x × 7x + x × 3
= 2x3 – 7x2 + 3x
= 3 × 3 – 1 × 3 – 3 × 1 + 1 × 1
=9 – 3 – 3 + 1 = 4
∴(a – b)2 = 4sq.units
[∵ (3 – 1)2 = 22 = 4]
(a – b)2 = a2 – 2ab + b2
Area of ABCD + Area of CYZS
= a2 – 2ab + b2
area of ABCD – area of BXYC – area of DCST + area of CYZS
= 5 × 5 – 2 × 5 – 2 × 5 + 2 × 2
= 25 – 10 – 10 + 4
= 9 sq.units
[∵ (5 – 2)2 = (3)2 = 9]
Question 4.
Add the product: a(a – b), b(b – c), c(c – a)
Solution:
a(a – b) + b(b – c) + c(c – a)
=a × a – a × b + b × b – b × c + c × c – c × a
=a2 – ab + b2 – bc + c2 – ca
=a2 + b2 + c2 – ab – bc – ca
Question 5.
Add the product: x(x + y – r), y(x – y+r), z(x – y – z)
Solution:
x(x + y – r) +y(x – y + r) + z(x – y – z)
= x2 + xy – xr + xy – y2 + yr + zx – yz – z2
= x2 – y2 – z2 + 2xy – xr + yr + zx – yz
Question 6.
Subtract the product of 2x(5x – y) from product of 3x(x+2y)
Solution:
3x(x + 2y) – 2x(5x – y)
=(3x × x + 3x × 2y)-(2x × 5x – 2x × y)
= 3x2 + 6xy – (10x2 – 2xy)
= 3x2 + 6xy- 10x2 + 2xy
= 8xy – 7x2
Question 7.
Subtract 3k(5k – l + 3rn) from 6k(2k + 3l – 2rn)
Solution:
6k(2k + 3l – 2m) – 3k(5k – l + 3m)
= 12k2+ 18kl – 12km – 15k2 + 3kl – 9km
= -3k2 + 21kl – 21km
Question 8.
Simplify: a2(a – b + c) + b2(a + b – c) – c2(a – b – c)
Solution:
a2(a – b + c) + b2(a + b – c) – c2(a – b – c)
= a3 – a2b + a2c + ab2 + b3 – b2c – ac2 + bc2 + c3
= a3 + b3 + c3 – a2b + a2c + ab2 – b2c – ac2 – bc2
Question 1.
Multiply the binomials:
(i) 2a – 9 and 3a + 4
(ii) x – 2y and 2x – y
(iii) kl + lm and k – l
(iv) m2 – n2 and m + n
Solution:
i) 2a – 9 and 3a + 4
(2a – 9) (3a + 4) = 2a (3a + 4) – 9(3a + 4)
= 6a2 + 8a – 27a – 36
= 6a2 – 19a – 36
ii) x – 2y and 2x – y
(x – 2y) (2x – y) = x(2x – y) – 2y(2x – y)
= 2x2 – xy – 4xy + 2y2
= 2x2 – 5xy + 2y2
iii) kl + lm and k – l
(kl + lm) (k – l) = kl(k – l) + lm(k – l)
= k2l – l2k + klm – l2m
iv) m2 – n2 and m + n
(m2 – n2) (m + n) = m2(m + n) – n2(m + n)
= m3 + m2n – n2m – n3
Question 2.
Find the product:
(i) (x + y)(2x – 5y + 3xy)
(ii) (mn – kl + km) (kl – lm)
(iii) (a – 2b + 3c)(ab2 – a2b)
(iv) (p3 + q3)(p – 5q+6r)
Solution:
i) (x + y) (2x – 5y + 3xy)
= x(2x – 5y + 3xy) + y(2x – 5y + 3xy)
= 2x2 – 5xy + 3x2y + 2xy – 5y2 + 3xy2
= 2x2 – 5y2 – 3xy + 3x2y + 3xy2
ii) (mn – kl + km) (kl – lm)
= kl(mn – kl + km) – lm(mn – kl + km)
= klmn – k2l2 + k2lm – lm2n + kl2m – klm2
iii) (a – 2b + 3c) (ab2 – a2b) = a(ab2 – a2b) – 2b(ab2 – a2b) + 3c(ab2– a2b)
= a2b2 – a3b – 2ab3 + 2a2b2 + 3ab2c – 3a2bc
= 3a2b2 – a3b – 2ab3 + 3ab2c – 3a2bc
iv) (p3 + q3) (p – 5q + 6r) = p3(p – 5q + 6r) + q3(p – 5q + 6r)
= p4 – 5p3q + 6p3r + pq3 – 5q4 + 6rq3
= p4 – 5q4 – 5p3q + 6p3r + pq3 + 6rq3
Question 3.
Simplify the following:
(i) (x-2y) (y – 3x) + (x+y) (x-3y) – (y – 3x) (4x – 5y)
(ii) (m + n) (m2 – mn + n2)
(iii) (a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
(iv) (pq-qr-i-pr) (pq-i-qr) – (pr-i-pq) (p-i-q – r)
Solution:
i) (x – 2y) (y – 3x) + (x + y) (x – 3y) – (y – 3x) (4x – 5y)
= (y – 3x) [x – 2y – (4x – 5y)] + (x + y)(x – 3y)
= (y – 3x) [x – 2y – 4x + 5y] + (x + y) (x – 3y)
= (y – 3x) (3y – 3x) + (x + y) (x – 3y)
= y(3y – 3x) – 3x(3y – 3x) + x(x – 3y) + y(x – 3y)
= 3y2 – 3xy – 9xy + 9x2 + x2 – 3xy + xy – 3y2
= 10x2 – 14xy
ii) (m + n) (m2– mn + n2)
= m(m2 – mn + n2) + n(m2 – mn + n2)
= m3 – m2n + n2m + nm2 – mn2 + n3
= m3 + n3
iii) (a – 2b + 5c) (a – b) – (a – b – c) (2a + 3c) + (6a + b) (2c – 3a – 5b)
= a(a – 2b + 5c) – b(a – 2b + 5c) – 2a(a – b – c) – 3c(a – b – c) + 6a(2c – 3a – 5b) + b(2c – 3a – 5b)
= a2 – 2ab + 5ac – ab + 2b2 – 5bc – 2a2 + 2ab + 2ac – 3ac + 3bc + 3c2 + 12ac – 18a2 – 30ab + 2bc – 3ab – 5b2
= – 19a2 – 3b2 – 34ab + 16ac + 3c2
iv) (pq – qr + pr) (pq + qr) – (pr + pq) (p + q – r)
= pq(pq – qr + pr) + qr(pq – qr + pr) – pr(p + q – r) – pq(p + q – r)
= p2q2 – pq2r + p2qr + pq2r – q2r2 + pqr2 – p2r – pqr + pr2 – p2q – pq2 + pqr
= p2q2 – q2r2 + p2qr + pqr2 – p2r + pr2 – p2q – pq 2
Question 4.
If a, b, care positive real numbers such that
Solution:
⇒ a + b = (ck + c) = c(k + 1) …………… (1)
Similarly b + c = a(k + 1) ……………(2)
c + a = b(k + 1) ………………..(3)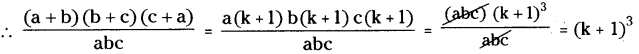
Exercise 11.4
Question 1.
Select a suitable identity and find the following products
(i) (3k + 4l)(3k + 4l)
(ii) (ax2 + by2)(ax2 + by2)
(iii) (7d – 9e)(7d – 9e)
(iv) (m2 – n2)(m2 + n2)
(v) (3t + 9s) (3t – 9s)
(vi) (kl – mn) (kl + mn)
(vii) (6x + 5)(6x + 6)
(viii) (2b – a)(2b +c)
Solution:
(3k + 4l) (3k 4l) = (3k + 4l)2 is in the form of (a + b)2.
=(3k)2 + 2 × 3k × 4l+ (4l)2 [ (a+ b)2 = a2 + 2ab + b2
= 3k × 3k + 24kl + 4l × 4l
= 9k2 + 24kl + 16l2
ii) (ax2 + by2) (ax2 + by2) = (ax2 + by2)2 is in the form of (a + b)2.
= (ax2)2 + 2 × ax2 × by2 + (by2)2 [ ∵ (a + b)2 = a2 + 2ab + b2]
= ax2 × ax2 + 2abx2y2 + by2 × by2
= a2x4 + 2ab x2y2 + b2y4
iii) (7d – 9e) (7d – 9e)
= (7d – 9e)2 is in the form of (a – b)2.
= (7d)2 – 2 × 7d × 9e + (9e)2 [ ∵ (a – b)2 = a2 – 2ab + b2]
= 7d × 7d – 126de + 9e × 9e
= 49d2 – 126de + 81e2
iv) (m2 – n2) (m2 + n2) is in the form of (a + b) (a – b).
∴ (a + b) (a – b) = a2 – b2
∴ (m2 + n2) (m2 – n2) = (m2)2 – (n2)2 = m4 – n4
v) (3t + 9s) (3t – 9s) = (3t)2 – (9s)2 [ ∵ (a + b) (a – b) = a2 – b2 ]
= 3t × 3t – 9s × 9s
= 9t2 – 81s2
vi) (kl – mn) (kl + mn) = (kl)2 – (mn)2 [ ∵(a + b) (a – b) = a2 – b2 ]
= kl × kl – mn × mn
= k2l2 – m2n2
vii) (6x + 5) (6x + 6) is in the form of
(ax + b) (ax + c).
(ax + b) (ax + c) = a2x2 + ax(b + c) + bc
(6x + 5) (6x + 6) = (6)2x2 + 6x (5 + 6) + 5 × 6
= 36x2 + 6x × 11 + 30
= 36x2 + 66x + 30
viii) (2b – a) (2b + c) is in the form of (ax – b) (ax + c).
(ax – b) (ax + c) = a2x2 + ax(c – b) – cb
(2b – a) (2b + c) = (2)2(b)2 + 2b (c – a) – ca
= 4b2 + 2bc – 2ab – ca
Question 2.
Evaluate the following by using suitable identities:
(i) 3042
(ii) 5092
(iii) 9922
(iv) 7992
(v) 304 × 296
(vi) 83 × 77
(vii) 109 × 108
(viii) 204 × 206
Solution:
i) 3042 = (300 + 4)2 is in the form of (a + b)2.
∵ (a+b)2 = a2 + 2ab + b2
a = 300, b = 4
(300 + 4)2 = (300)2 + 2 × 300 × 4 + (4)2
= 300 × 300+ 2400 + 4 × 4
= 90,000 + 2400 + 16
= 92,416
ii) 5092 = (500 + 9)2
a = 500, b = 9
= (500)2 + 2 × 500 × 9 + (9)2
[ ∵ (a + b)2 = a2 + 2ab + b2]
= 500 × 500 + 9000 + 9 × 9
= 2,50,000 + 9000 + 81
= 2,59,081
iii) 9922 = (1000 – 8)2
a = 1000, b = 8
= (1000)2 – 2 × 1000 × 8 + (8)2 [∵ (a-b)2 = a2 – 2ab + b2]
= 1000 × 1000 – 16,000 + 8 × 8
= 10,00,000 – 16000 + 64
= 10,00,064 – 1600
= 9,98,464
iv) 7992 = (800 – 1)2
a = 800, b = 1
= (800)2 – 2 × 800 × 1 + (1)2
= 800 × 800 – 1600 + 1
= 6,40,000 – 1600 + 1
= 6,40,001 – 1600
= 6,38,401
v) 304 × 296 = (300 + 4) (300 – 4) is in the form of (a + b) (a – b).
(a + b) (a – b) = a2 – b2
∴ (300 + 4) (300 – 4) = (300)2 – (4)2
= 300 × 300 – 4 × 4
= 90,000 – 16
= 89,984
vi) 83 × 77 = (80 + 3) (80 – 3)
= (80)2 – (3)2 [ ∵ (a + b) (a – b) = a2 – b2]
= 80 × 80 – 3 × 3
= 6400 – 9
= 6391
vii) 109 × 108 = (100 + 9) (100 + 8)
= (100)2 + (9 + 8)100 + 9 × 8
= 10,000 + 1700 + 72
= 11,772
viii) 204 × 206 = (205 – 1) (205 + 1)
= (205)2 – (1)2 [∵ (a + b)(a-b) = a2 – b2]
= 205 × 205 – 1 × 1
= 42,025 -1
= 42,024

